Course en VTT

Josselyn participe à une descente chronométrée sur une piste de VTT. Un radar pédagogique a été installé à mi-parcours pour afficher la vitesse des participants, afin de les sensibiliser à leur allure.

Malheureusement, le radar ne fonctionne pas. Cependant, un capteur placé au départ a enregistré la distance parcourue par Josselyn (en mètres) en fonction du temps (en secondes). Cette distance parcourue est modélisée par la fonction : \(f(t)=−0,2t^3+2t^2\) pour \(t ∈ [0;10]\).

Le radar, placé à 6 secondes, permet d’attribuer un bonus de temps si la vitesse dépasse 12 m/s à cet endroit précis.

Problématique : Josselyn peut-il bénéficier de ce bonus à cet instant précis ?

1. Que représente la fonction \(f\) ? À quoi correspond la variable \(t\) ?

2. D'après le graphique ci-dessous, quelle est la vitesse atteinte par Josselyn à 3,5 s ?

3. La droite qui passe par le point B représente la tangente à la courbe au point d'abscisse 3,5. Déterminer graphiquement le coefficient directeur de la droite (arrondir au centième près).

Coup de pouce 1 : une perle est là pour vous aider à déterminer graphiquement le coefficient directeur d'une droite.

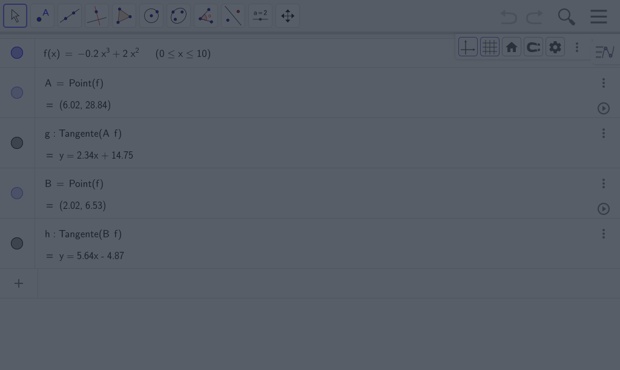
4. On a tracé la courbe de la fonction `f` avec GeoGebra, et affiché la droite tangente au point B d'abscisse 3,5.

a. Relever dans la fenêtre algèbre, l'équation de la droite tangente.
b. En déduire la valeur du coefficient directeur de cette droite.
c. Comparer cette valeur à la réponse de la question 3. 

5.  Le coefficient directeur de la droite tangente à la courbe de la fonction \(f\) en un point d'abscisse \(a\) représente le nombre dérivé de la fonction \(f\) en ce point d'abscisse \(a\). On le note \(f'(a)\). En déduire le nombre dérivé au point d'abscisse \(x = 3,5\).

6. Avec GeoGebra :

a. Tracer la tangente au point A d'abscisse 6.

Coup de pouce 2 : une perle est là pour vous aider si besoin !

b. Dans la fenêtre algèbre, relever l'équation de la droite tangente à la courbe au point d'abscisse 6.
c. En déduire le nombre dérivé au point d'abscisse 6.

d. Déterminer l'équation de la tangente au point d'abscisse 6.

Coup de pouce 3 : une perle est là pour vous aider à déterminer l'équation de la tangente en un point de la courbe de la fonction !

7. Le nombre dérivé correspond à la vitesse de Josselyn en VTT. En déduire la vitesse atteinte au bout de 6 s.

8. Répondre à la problématique.